El examen de matemáticas en la EBAU de Madrid sí se puede resolver, aunque hay discusión sobre un enunciado

Varios medios de comunicación han publicado que uno de los ejercicios del examen de matemáticas que aparecía en las pruebas de acceso a la universidad (EBAU) de Madrid era “imposible de resolver”. Estas noticias se basan en las críticas de un doctor en física que, en rigor, se centraban en el planteamiento de uno de los enunciados. Como explican él mismo y otros expertos consultados por Newtral.es, el problema al que se enfrentaron los estudiantes madrileños sí tiene solución y se ajusta al nivel exigido en bachillerato.

Se trata del examen de Matemáticas II que hicieron los alumnos y alumnas madrileñas de la rama de ciencias. El ejercicio B.2 constaba de una función real de variable real en la que se pedía, entre otras cosas, “estudiar la continuidad de la función en R”. Para los no instruidos en matemáticas, estudiar la continuidad de una función real es —simplificando mucho— indicar si es continua o discontinua y, en todo caso, en qué puntos.

La discusión se presenta a la hora de pedir a los estudiantes que estudien la continuidad “en R”, forma que se refiere a todos los números reales. El quid de la cuestión es que se trata de una función continua, pero con una asíntota en ‘x=1’. Es decir, el valor 1 de ‘x’ no está en el dominio de la función, como indican los especialistas consultados y se muestra en la siguiente gráfica.

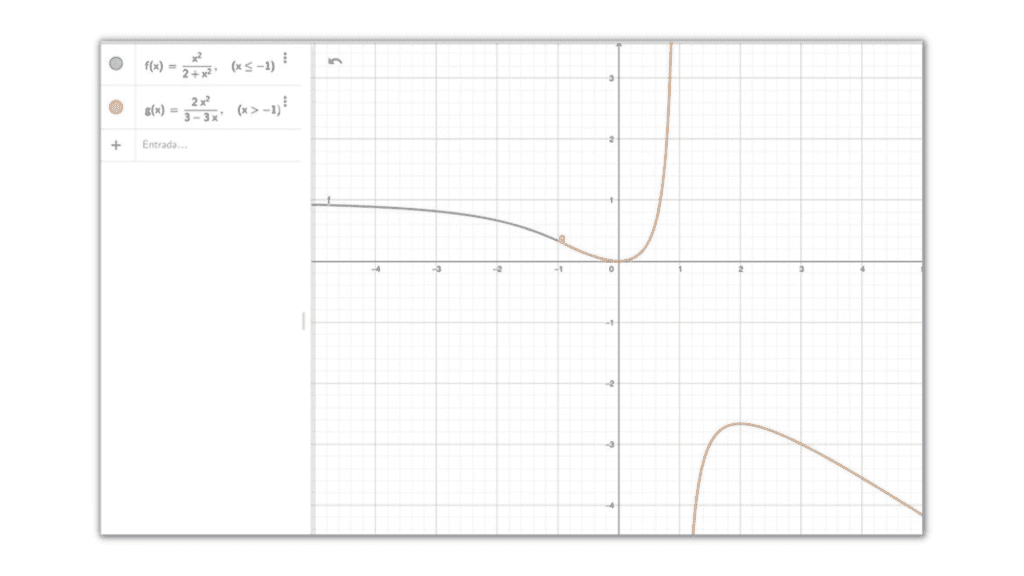
Por tanto, ‘x=1’ no pertenece al dominio de la función, por lo que no se podría decir ni que es continua ni que no lo es, sino que hay una discontinuidad. “En mi opinión, la forma correcta de formular el ejercicio hubiera sido estudia la continuidad de la función y las discontinuidades en R. De esta forma se está diciendo que estudies los puntos que no están en el dominio como ‘x=1’”, explica a Newtral.es el doctor en física teórica Sergio Montañez, profesor de instituto.

A su juicio, la formulación que aparecía en el examen es “como preguntar si el actual rey de Francia es calvo o no es calvo” —Francia es una república— y “para resolver el ejercicio es necesario sobreentender cosas que el enunciado no dice explícitamente”.

Tres expertos matemáticos coinciden en que el ejercicio del examen no es “imposible“ y tiene solución

Sin embargo, otros expertos en la materia entienden que, cuando se pregunta por la continuidad de la función, se sobreentiende que el ejercicio abarca las discontinuidades y que, por tanto, el alumno debe expresar que, en este caso, no hay ningún valor en ‘x=1’, dada la asíntota que presenta la función y que se trata de una discontinuidad.

José Ignacio de la Fuente Domínguez, profesor de matemáticas del IES Giner los Ríos de Alcobendas, considera que el ejercicio está bien formulado para un estudiante de bachillerato. “Cuando se pide estudiar la continuidad se trata de decir si una función es o no continua. Se sobreentiende que el hecho de estudiar la continuidad incluye la continuidad y la discontinuidad”, indica en conversación telefónica con Newtral.es.

“La forma de resolverlo es hallar los límites laterales y ver si son iguales o no. En este caso no son iguales y, por tanto, puedo concluir que no es continua. No me preguntan qué tipo de discontinuidad presenta, por lo que no tendría por qué explicar que hay una asíntota. Otra cosa es que el alumno quiera explicar qué tipo de discontinuidad tiene y explique que hay un límite de ‘y’ hacia el infinito y que presenta una asíntota vertical, pero al decir que los límites son distintos y que la función no es continua se responde a la pregunta planteada”, sostiene este profesor.

Esther García, editora del Boletín de la Real Sociedad Matemática Española (RSME) y profesora de matemática aplicada en la Universidad Rey Juan Carlos (URJC), también opina que “el enunciado de este ejercicio es clásico” y que “los alumnos que se saben el tema entienden perfectamente el enunciado”. En este sentido, asegura que “no es un problema irresoluble” y que, aunque se puede enunciar de otras formas, los estudiantes deben estudiar, además del punto ‘x=1’ —punto donde la función es discontinua por la presencia de la ya mencionada asíntota—, los intervalos abiertos desde menos infinito a 1 y desde 1 a infinito, intervalos en los que la función es continua.

En cualquier caso, los tres expertos consultados —José Ignacio de la Fuente, Esther García y Sergio Montañez— coinciden en que en ningún caso se puede afirmar que el ejercicio del examen de matemáticas sea “imposible de resolver”, en contra de lo que han publicado multitud de medios de comunicación, sino que —en todo caso— puede existir una discusión académica respecto a la formulación del enunciado. Para García, la posición de Montañez sobre la posible imprecisión del enunciado es “una observación si se quiere ser muy riguroso”, pero que no afectaría a la resolución del ejercicio.

[Así es la nueva EBAU que se prueba en un proyecto piloto]

Los medios que publicaron que el ejercicio planteado en el examen de selectividad de Madrid no tenía solución se basaban en una serie de tuits publicados, precisamente, por el físico Sergio Montañez. Pero este experto nunca dijo que el ejercicio no se pudiera resolver, sino que “no se puede estudiar la continuidad en x=1 porque ese punto no pertenece al dominio de la función”. Este profesor se queja de que los medios publicaron una noticia sobre su crítica sin haber contactado con él y, en un artículo en su blog, afea que publicaran que el ejercicio no tenía solución. De hecho, ha remitido a Newtral.es lo que, a su juicio, habría sido una respuesta correcta con la formulación que tenía el ejercicio.

Para la formulación que él sugiere —que tan solo supone preguntar por “las discontinuidades en R”, no solo por la continuidad— nos remite otra respuesta que, en esencia, coincide con la planteada por los profesores José Ignacio de la Fuente y Esther García. Es decir, que se trata de una función con una discontinuidad en ‘x=1’ donde ‘f(x)’ tiende al infinito.

En definitiva, no es correcto afirmar que uno de los ejercicios del examen de matemáticas al que se enfrentaron los estudiantes madrileños en la EBAU era “imposible de resolver” o que no hubiera solución. Los medios de comunicación que publicaron esta versión malinterpretaron las críticas de un doctor en física teórica que, en realidad, sugería otro planteamiento en la formulación del ejercicio. Tanto él como otros expertos consultados por Newtral.es, incluida una portavoz de la Real Sociedad Matemática Española, coinciden en que el problema tiene solución y que se adapta a los contenidos del currículo de bachillerato.